How I Rebalance My Portfolio

The Art of Portfolio Optimization

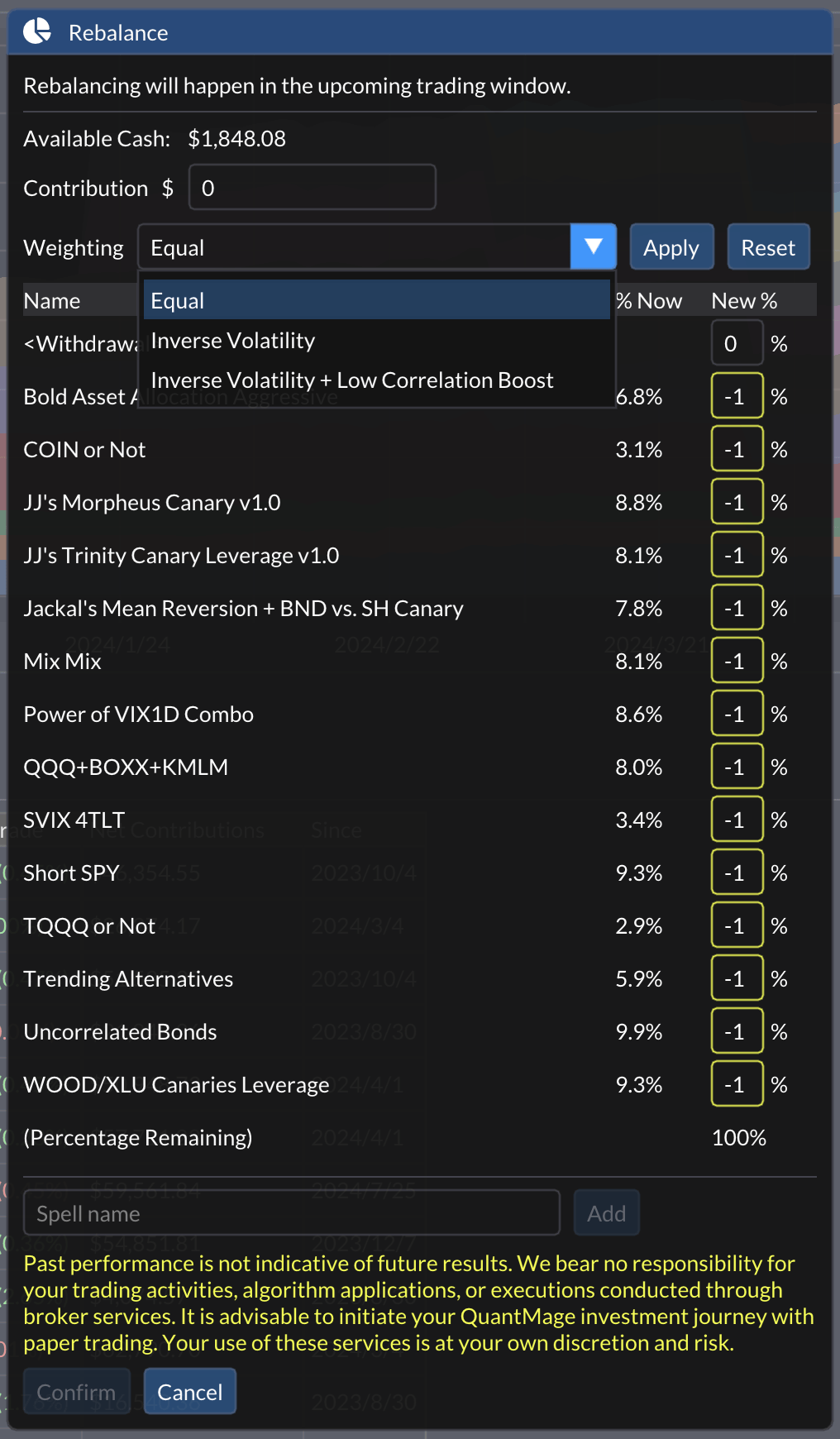
QuantMage takes care of most of your investment and trading decisions, but portfolio-level rebalancing is still in your hands. Personally, I used to check each strategy’s historical volatility and weight them inversely: the less volatile, the higher the weight. Simple enough, right? However, this approach doesn’t consider correlations between strategies. So, I developed a tweak called the Low Correlation Boost. By combining this with the strategy’s inverse volatility factor, I got a more balanced final weight. As you can imagine, this manual process was tedious, so I integrated this new feature into QuantMage.

Inverse Volatility + Low Correlation Boost

Now, QuantMage offers Equal Weighting (EW), Inverse Volatility (IV), and Inverse Volatility + Low Correlation Boost (IV+LCB). The feature automatically backtests each strategy, computes their volatilities and correlations, and determines the weights. Since some factors can’t be captured by simple equations, you might want to fix some strategy weights to your liking and let the feature calculate the rest. You can manually set some weights and let the tool handle the rest. For more details about this feature, check here.

Portfolio Optimization

If you’ve dabbled in portfolio optimization before, you’ve likely heard about the mean-variance framework. Developed by Harry Markowitz, this framework is a cornerstone of modern portfolio theory. It aims to construct an optimal portfolio by balancing return (mean) and risk (variance). Think of the Sharpe Ratio. This framework helps investors select a mix of assets that maximizes expected return for a given level of risk or minimizes risk for a given level of expected return, creating a diversified portfolio on the efficient frontier.

Understanding Different Optimization Approaches

Minimum Variance (MV): This approach aims to minimize the overall portfolio variance. However, while it focuses on reducing volatility, it might compromise on diversification.

Equally-weighted Risk Contributions (ERC): Also known as Risk Parity, ERC aims to equalize the risk contributions of all assets. It strikes a balance between diversification and volatility. ERC can be seen as Inverse Beta Weighting: the lower a strategy’s beta to the portfolio, the higher its allocation. For a deeper dive into ERC, check out this helpful paper.

Both MV and ERC involve complex optimization math. ERC doesn’t have an analytical solution, requiring numerical approaches. My IV+LCB heuristic approximates ERC with a simpler method. For now, I’m satisfied with these simpler approaches because complex math doesn’t always lead to better performance in practice. If you want to explore more about portfolio optimization and understand when each approach works best, I highly recommend this article.

Why Returns Are Not Considered

You might notice none of these approaches consider returns, focusing solely on the variance part of the mean-variance framework. Some argue that returns are noisier and less predictable than risks measured as volatility. Personally, I prefer to be conservative and focus on risk when it comes to position sizing. Returns are crucial when deciding whether to include a strategy in my portfolio, but once included, I focus on the risk component.

I use the calculated weights as a starting point and often adjust them based on other considerations. The timing of rebalancing remains discretionary. As I continue to learn, my weighting approach will likely evolve. How are you currently rebalancing your portfolio? Which weighting or rebalancing approach mentioned above appeals the most to you? Please leave a comment!