Compounding, Volatility, and The Art of Leverage
Navigating the Curious World of Levered ETFs
Some argues that a leverage can be a good thing even for long-term investors while many others say you’d better steer clear of it. This one argues a sweet spot for leverage hovers around 2x, especially for the US market. And yes, we've got those spicy levered ETFs (up to 3x) ready to serve up some leverage on a silver platter for both indexes and individual stocks. Enter HEDGEFUNDIE’s excellent adventure and its burgeoning fan club, proving that playing with leverage has gone mainstream. Even a subreddit for it. Yet, here's the twist: the performance of levered ETFs over the long haul can sometimes feel like a wild ride that doesn't exactly match up with what you signed up for. It’s because those ETF products are engineered to achieve the leverage effect per day. It’s understandable why such a goal is mandated once you consider constant inflows & outflows of investor money into such a product. You might ask, “Ok, if an ETF achieves, let’s say, 3x levered return per day, I can assume 3x performance of the underlying over a longer period, too, right?” The answer is no and it’s due to compounding effect and volatility drag.
The Magic of Compounding
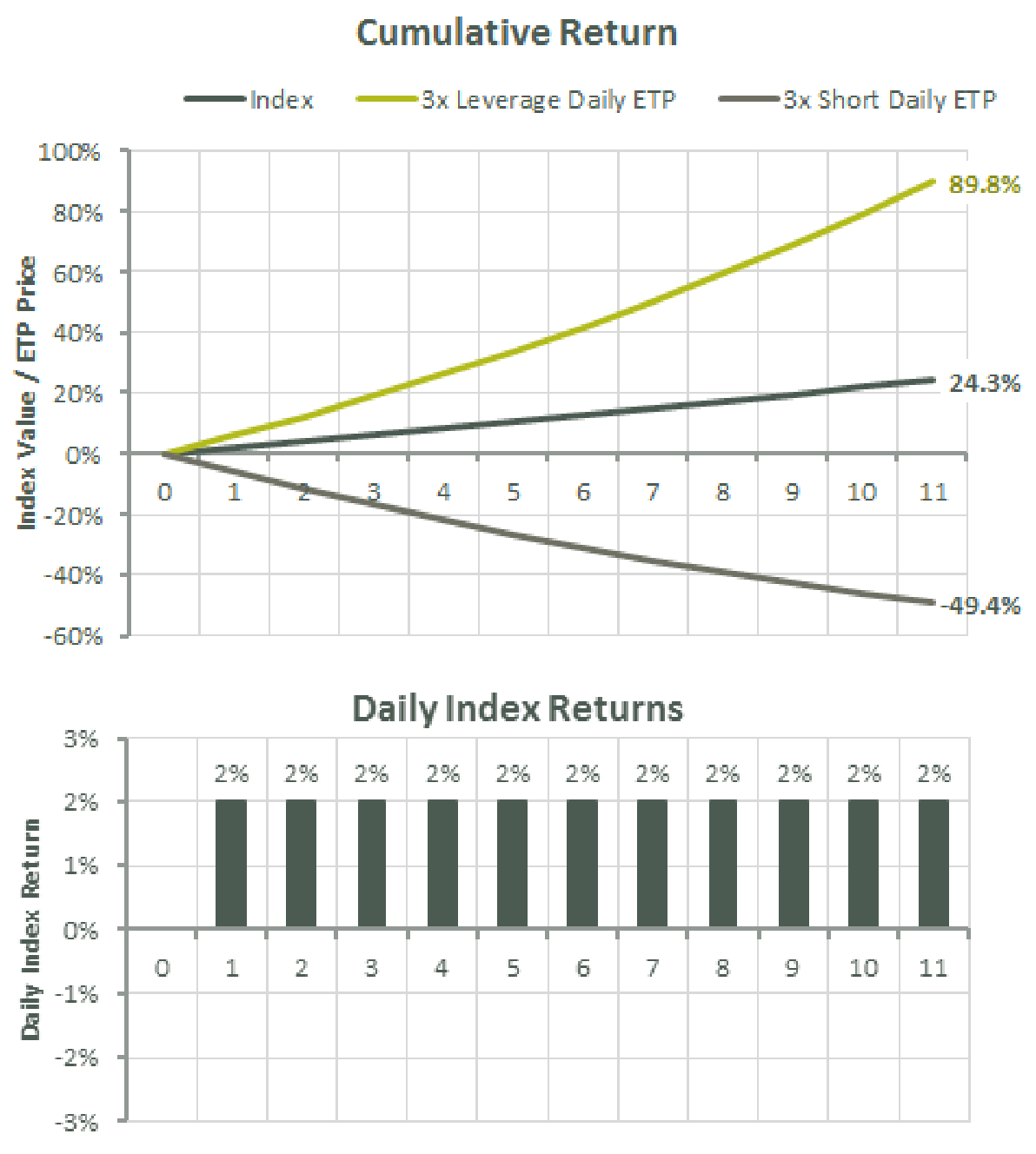
Daily returns are compounded. In other words, the accumulation is geometric (multiplicative) than arithmetic (additive). Today’s 2% gain will be bigger in absolute terms than the same 2% gain yesterday since the starting amount is bigger. Imagine an investment magically churning a consistent 2% gain every day for 11 days. Arithmetic says you get a 22% (= 0.02 * 11) return, but the magic of compounding delivers a 24.3% (≈ 1.02^11 - 1) return instead. Now, throw in some 3x leverage into this mix, and instead of tripling your expectations to 72.9% (= 3 * 24.3), you're looking at an 89.8% (≈ 1.06^11 - 1) return. Leverage amplified compounding. Mind blown, right?
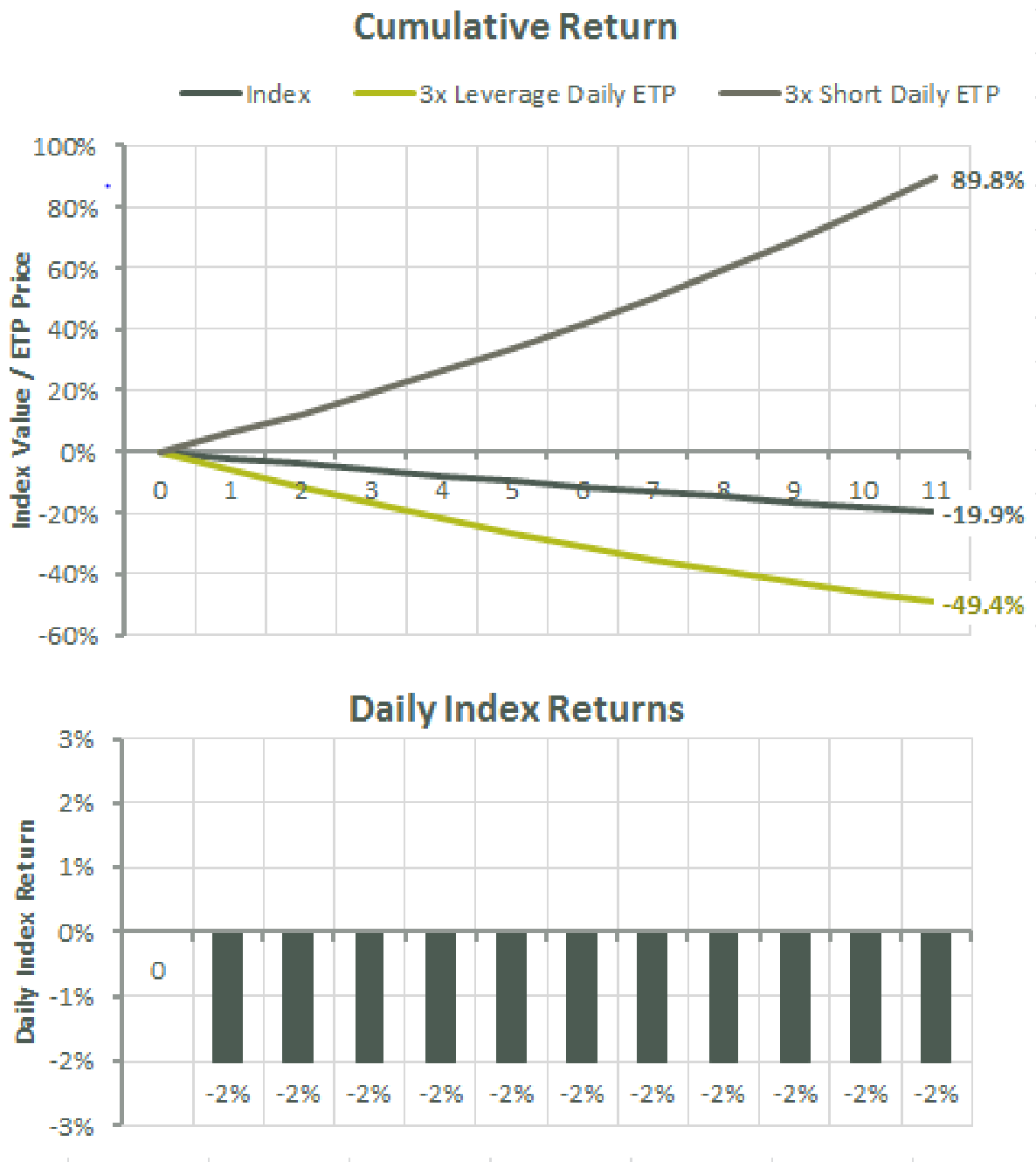
Compounding applies even if daily returns are negative. Consider the parallel case of the above, but with 2% daily losses. Again, its 11-day return is -19.9% (≈ 0.98 ^ 11 - 1), not -22% (= -2 * 11). And its 3x leverage shows a less worse return of -49.4% (≈ 0.94 ^ 11 - 1) than the naively expected -59.7% (= 3 * -19.9). It’s called the 8th wonder of the world for a reason.
By the way, these examples and their plots are from this excellent document from WisdomTree.
The Sneaky Volatility Drag
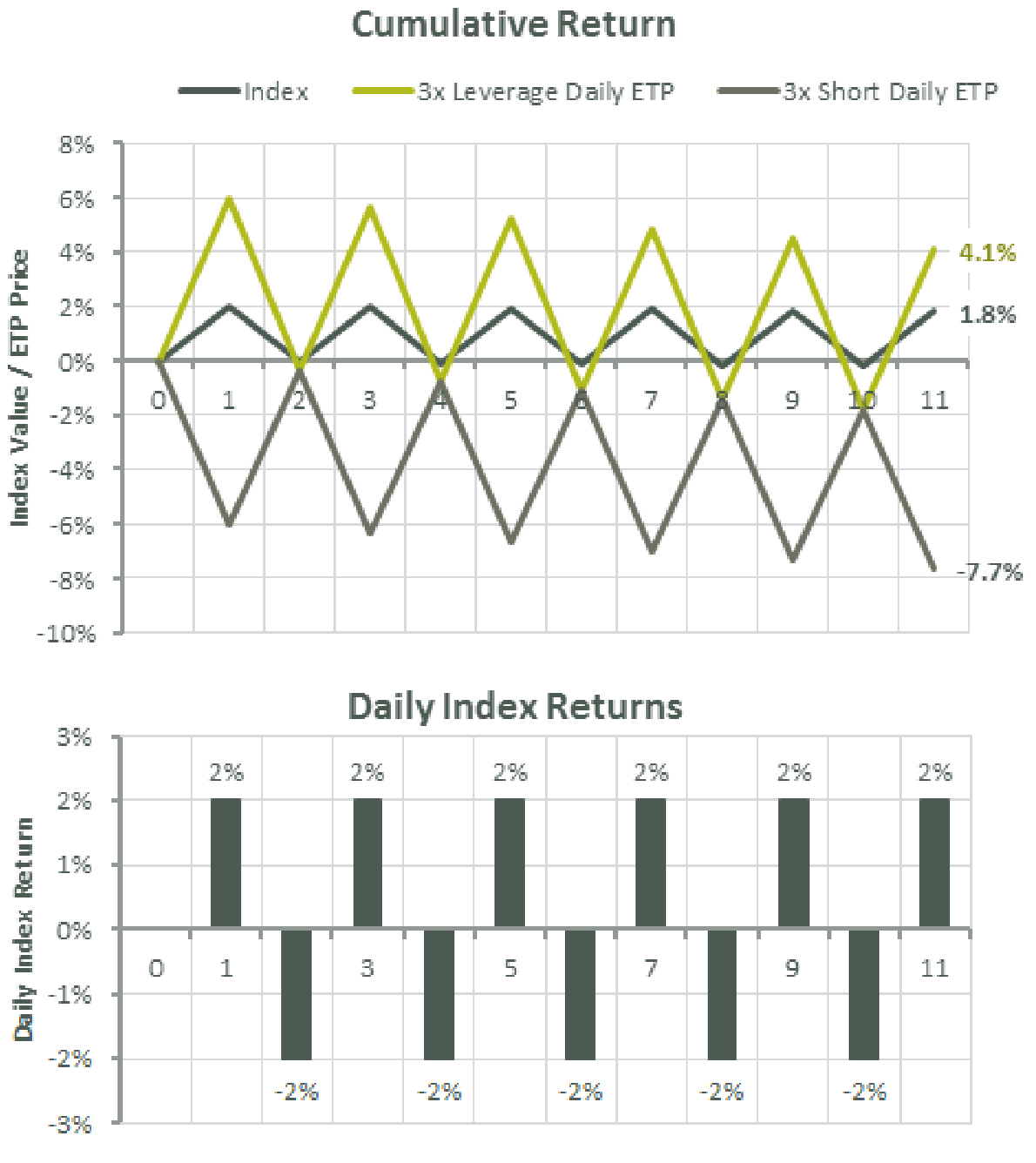
Ok, so compounding is like magic that keeps giving a better-than-expected return for both uptrend and downtrend markets, right? Not so fast. Stocks doesn’t usually go either straight up or down. They fluctuate. They tend to be volatile. Let’s see then a slightly more realistic case of having daily returns alternating between 2% and -2%. Our naive (i.e. additive) intuition tells us that each day will cancel each other out except the last 2% return, producing 2% over the 11 days. But surprise, it's actually 1.8%. And if you're riding this roller coaster with 3x leverage, you'd expect a 5.4% (= 1.8 * 3) gain but only end up with 4.1%. Why didn’t the compounding do its magic here?
Compounding (geometric accumulation) is still happening here. The fallacy lies in your assumption that 2% loss can be compensated by 2% gain. You need 2.04% gain to compensate it. It’s helpful to think about an extreme case. For instance, you need 100% gain, not 50%, to compensate 50% loss. Once realizing this, you can now understand why the zigzagging lines above show slight downtrends overall instead of remaining flat. This is what they call Volatility Drag or Volatility Tax. And, as you see, a leverage exacerbates the drag by amplifying underlying volatility. With compounding effect and volatility drag, it becomes clear why daily 3x leverages won’t imply the same leverage ratio for a longer term.
Finding Your Leverage Sweet Spot
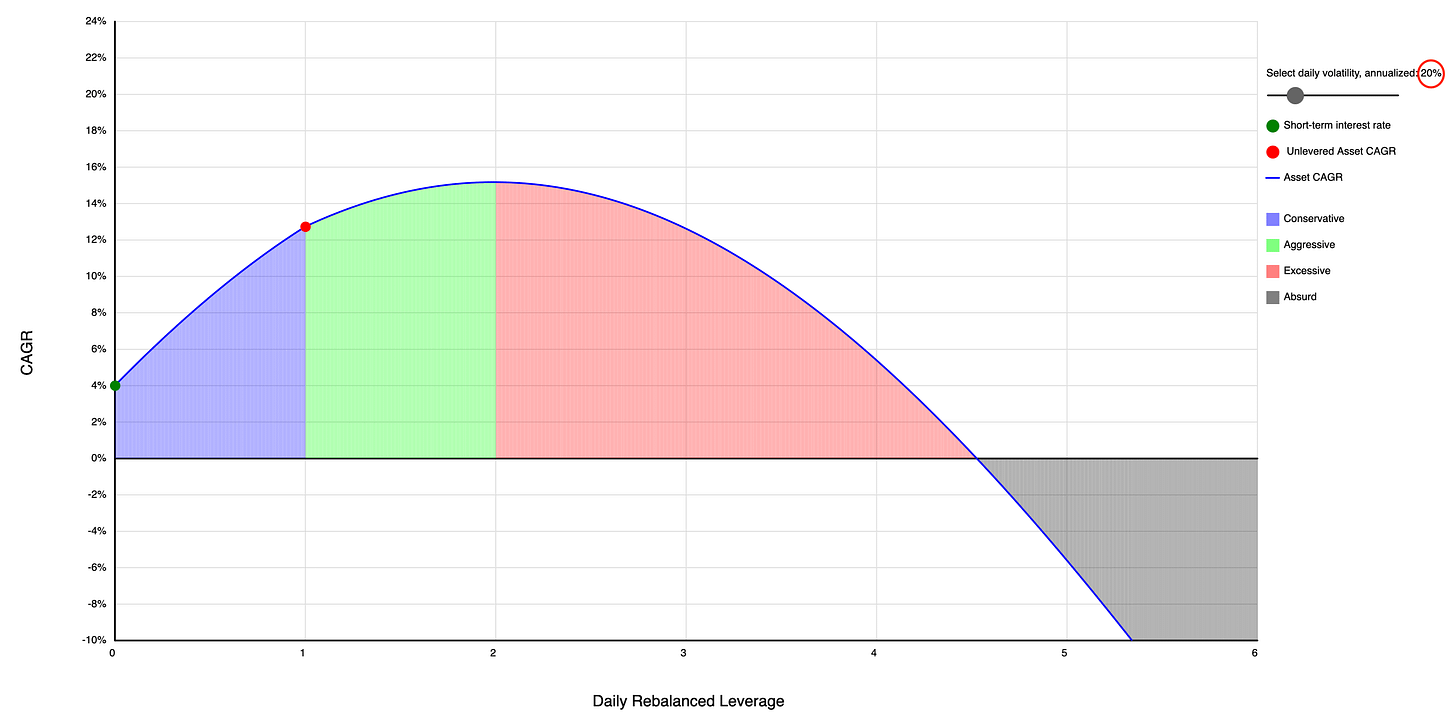
So, the million-dollar question: To lever or not to lever? It's all about the balance between expected returns and how wild the ride (volatility) is. There's this neat tool that shows you the optimal leverage ratio based on these factors:
With an annual return of 12.73% and a volatility of 20%, you get an optimal leverage ratio of 2 here. As either its annual return decreases or its volatility increases, the optimal leverage gets lower:
The optimal leverage can even get less than 1 (which means you’d better de-lever the underlying by mixing it with cash or a cash-like asset) when the volatility gets high enough:
Please note that we’re talking about the optimality for the purpose of maximizing its annual return here. There is also another knob that affects, the short-term interest rate, since borrowing for leverage is not free. I ignored it here for the sake of simplicity.
In Summary
Compounding defies our naive arithmetic of a long-term return.
Volatility drag is another manifestation of compounding that belies our intuition and can give us a return that is much lower than what our naive mental arithmetic produces.
Leverage just amplifies these effects.
The Takeaway
Now you have a formula to come up with an optimal leverage ratio given an underlying. Still understanding the optimal leverage ratio is more art than science, as the market's mood swings can change the game. That’s where nimbler tactical asset allocation approaches can outshine static asset allocation ones like HEDGEFUNDIE’s above. And there is no better tool for them than QuantMage in my biased opinion :)
Compounding is a fascinating topic. The rabbit hole goes deeper as you dig into it, extending to the interesting subjects, such as arithmetic mean of returns vs. geometric mean (the latter is often approximated by the former minus a half of volatility), log returns, and ergodicity. And who knows? Our next adventure might just take us deeper into these fascinating warrens.



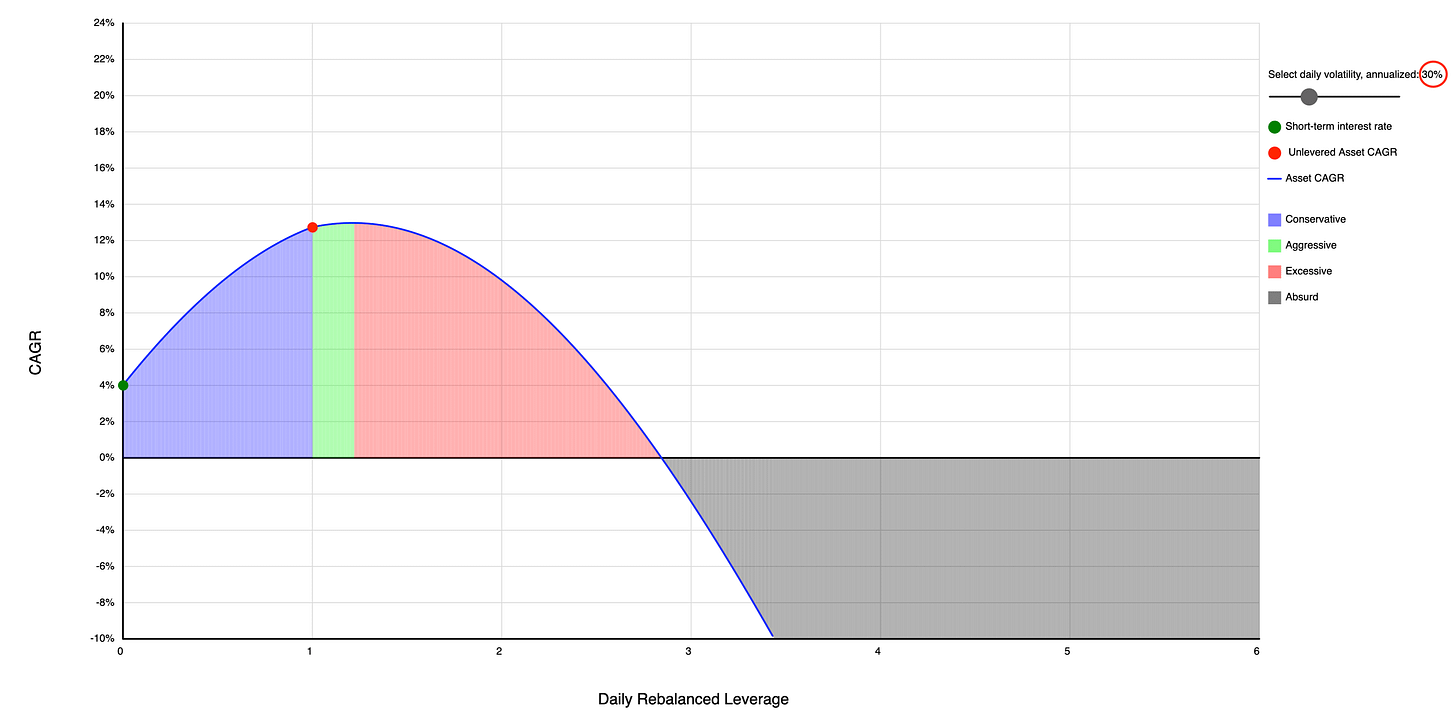
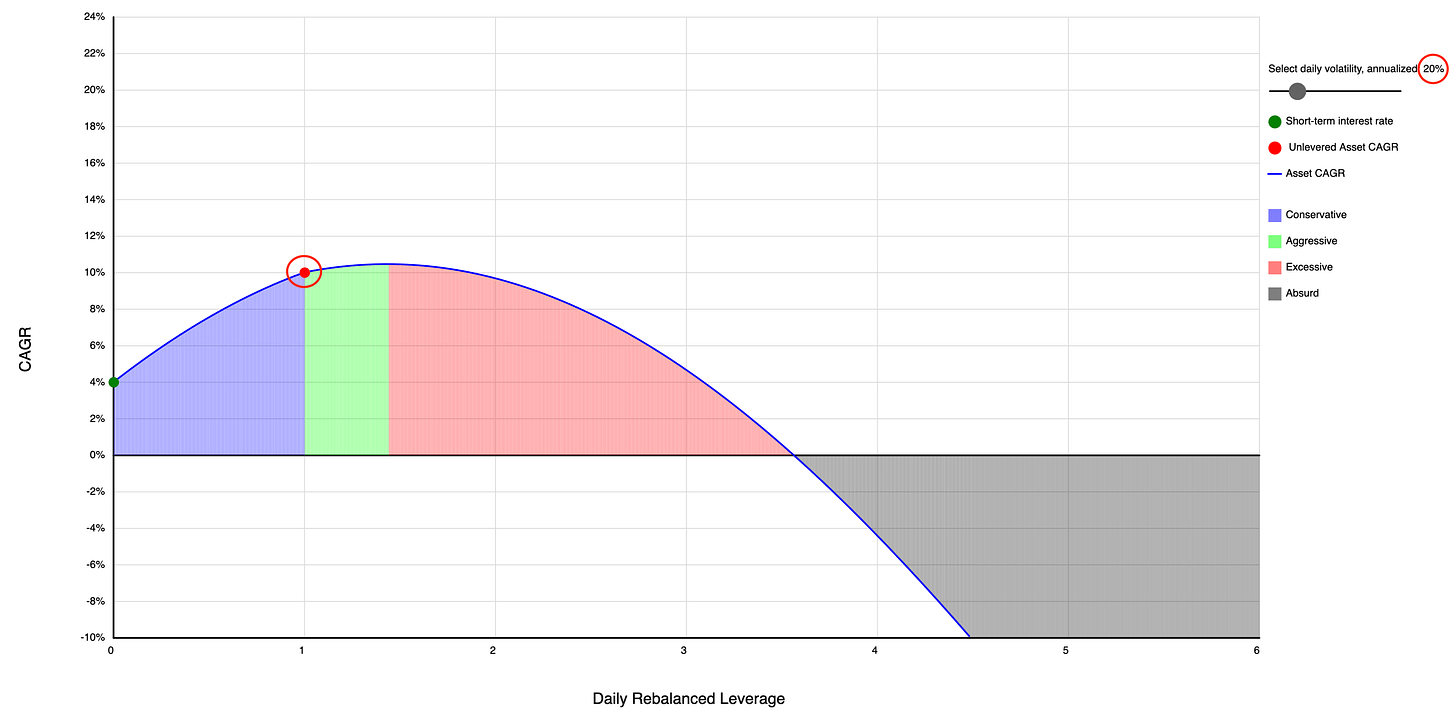
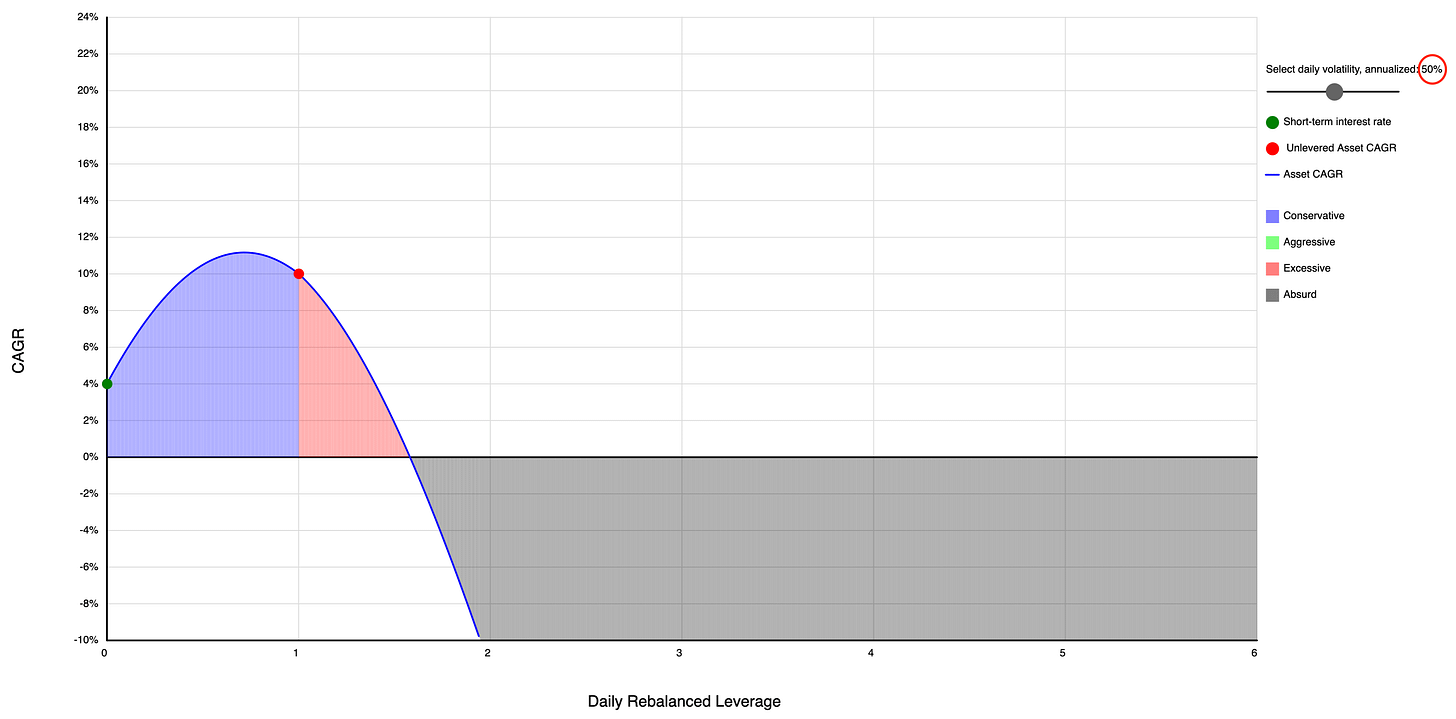
Optimal amount seems to go up if you're using advanced automated YOLO strategies.
The other bit of art comes from Shannon's Demon and rebalancing...